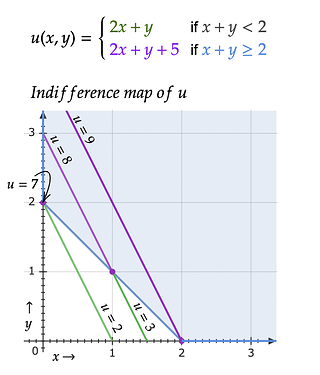
Problem. Find demand for this utility function:
u(x,y) = \begin{cases} 2x+y & \text{if } x+y < 2 \\ 2x+y+5 & \text{if } x+y\geq 2\end{cases}
Here is the problem we need to solve:
\displaystyle \max_{x\geq 0,y\geq 0} \ u(x,y) \\ \text{s.t. } \ p_Xx+p_Yy\leq M
Solution. Indifference Map of utility function u looks like this:
To find the demand, we consider the following cases:
Case 1: either \max\left(\dfrac{M}{p_X},\dfrac{M}{p_Y}\right)< 2 or \min\left(\dfrac{M}{p_X},\dfrac{M}{p_Y}\right)\geq 2
In this case, demand is given by
(x^d,y^d)\in\begin{cases}\left\{\left(\dfrac{M}{p_X},0\right)\right\} & \text{if } p_X<2p_Y \\ \left\{\left(0,\dfrac{M}{p_Y}\right)\right\} & \text{if } p_X>2p_Y \\ \left\{\left(x,y\right)\in\mathbb{R}^2_+|p_Xx+p_Yy=M\right\} & \text{if } p_X=2p_Y\end{cases}
Case 2: \max\left(\dfrac{M}{p_X},\dfrac{M}{p_Y}\right)\geq 2 and \min\left(\dfrac{M}{p_X},\dfrac{M}{p_Y}\right)< 2
In this case, demand is given by
(x^d,y^d)\in\begin{cases}\left\{\left(\dfrac{M}{p_X},0\right)\right\} & \text{if } M\geq 2p_X \\ \left\{\left(0,\dfrac{M}{p_Y}\right)\right\} & \text{if } M <2p_X \text{ and }p_X>2p_Y \\ \left\{\left(\dfrac{M-2p_Y}{p_X-p_Y},\dfrac{2p_X-M}{p_X-p_Y}\right)\right\} & \text{if } M <2p_X \text{ and }p_X < 2p_Y \\ \left\{\left(x,y\right)\in\mathbb{R}^2_+|p_Xx+p_Yy=M, x+y\geq 2\right\} & \text{if } M <2p_X \text{ and }p_X=2p_Y\end{cases}