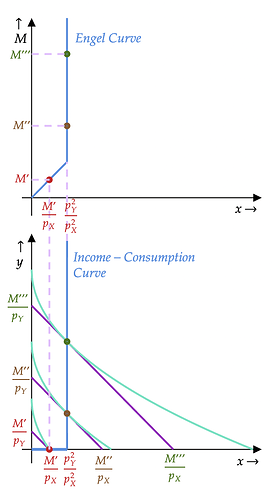
A Note on the Income Consumption Curve and the Engel curve
Consider the following consumer’s utility maximisation problem (UMP):
\max_{x\geq 0, \ y\geq 0} \ u(x,y) \\ \text{s.t. } \ p_Xx + p_Yy \leq M
where the prices p_X > 0, p_Y > 0 and M \geq 0 are given.
Solution to the above problem in known as demand which can depend on p_X, p_Y, M.
Fix p_X,p_Y and the set of demands for X and Y as we vary M in the (x,y)-plane is the income-consumption curve (ICC).
Formally, fix p_X,p_Y,
ICC for X = \{(x^d,y^d)\in\mathbb{R}^2_+|(x^d,y^d) \text{ solves UMP for some } M\}
Engel curve of commodity X is in the (x, M)-plane. Again, we fix p_X, p_Y,
Engel curve for X = \{(x^d,M)\in\mathbb{R}^2_+|(x^d,y^d) \text{ solves UMP for income } M \text{ for some } y^d\in\mathbb{R}_+\}
As an example, consider u(x,y) = 2\sqrt{x}+y. Solving UMP
\max_{x\geq 0, \ y\geq 0} \ 2\sqrt{x}+y \\ \text{s.t. } \ p_Xx + p_Yy \leq M
we get the Engel curve for X as x = \min\left(\dfrac{M}{p_X},\dfrac{p_Y^2}{p_X^2}\right) which is plotted in the (x,M)-plane, and we get the income-consumption curve as set of (x,y)-points satisfying \min\left(y,\dfrac{p_Y^2}{p_X^2}-x\right)=0 which is in the (x,y)-plane.
Here is the picture: